在上一篇文章，我們介紹了線性回歸與感知器，現在讓我們來認識ML中最重要的神經網路以及決策樹吧！

多層感知器，可行嗎?

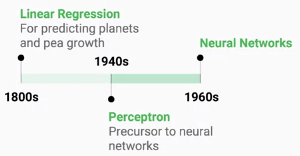
上篇文章中，我們討論到了感知器，但感知器為何不能是多層呢?多層的感知器會出現怎樣的效果呢?多層的感知器聽起來很猛，但事實上如果不使用非線性的激活函數(activation function)，多層感知器是可以被壓縮成單層感知器的，所以也就沒有差別。

使用非線性的激活函數來解決!

因此，我們需要非線性的激活函數。這時，像Sigmoid函數，或是像雙曲正切(hyperbolic tangent)函數，也稱為tanh函數正是我們所需要的。目前為止我們的討論都限定在可微分的函數，因為這能讓我們在反向傳播(back propagation)時獲得模型權重(weights)。而過去因為激活函數限定使用可微(differentiable)函數，使得神經網路難以訓練。而模型效能本身也受到數據量、算力以及其他訓練過程中的困難所限制。譬如說我們在訓練的過程中常常進入到鞍點(saddle points)，導致在梯度下降的過程中無法順利找到全局最優解。但是，一旦使用了ReLU函數等技巧，便能實現8-10倍的訓練速度，也幾乎能確保邏輯回歸(logistic regression)的收斂性(convergence)。

前饋神經網路的行成

建立多層感知器，其實就和大腦一樣，我們可以透過連接許多感知器來形成層(layer)，製造一個前饋神經網路(feedforward neural network)。這和單層感知器實際上沒有太大區別，仍然有輸入、加權總和、激活函數和輸出。其中一個區別是非輸入層中的神經元的輸入不是原始輸入而是前一層的輸出(聽起來有夠拗口，但就是人行蜈蚣的概念，後面的神經元是吃前面神經元的輸出而不是最初的輸入)。另一個不同之處在於它連接層之間的神經元的方式不再是向量(vector)，而是矩陣(matrix)，因為層之間所有神經元皆有完全連接的性質。

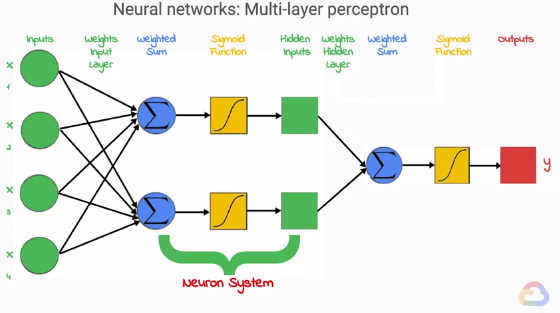
在上圖中，輸入層權重矩陣是4╳2，隱藏層權重矩陣是2╳1。後面我們會學到，神經網路事實上並不總是完全連接的，且有著驚人的運用與表現。每個非輸入神經元(non-input neuron)，你可以將其視為一個單元中的三個步驟的集合。第一步是加權和，第二步是激活函數，第三步是激活函數的輸出。(待更)

若是覺得本文有幫助，歡迎點選Like、星星收藏或是追蹤系列文支持哦！